Time-Series Analysis and Forecasting

  시계열(time-series) 데이터를 분석하고 그 결과를 기반으로 향후 흐름을 예측하고자 하는 노력은 다양한 분야에서 지속적으로 이루어져 왔습니다. 주가 예측도 마찬가지겠지요.

  이번 글에서는 주가 예측을 위한 한 가지 방법을 소개하고, 실제 구현하여 테스트한 결과를 공개하고자 합니다. 과거에 발표되었던 논문을 기준으로 한 것이며, 이 방법에 의한 예측 결과를 실제 투자의 기준으로 활용하는 것은 부적절함을 미리 알립니다.

  ※ 참고 논문: Tai-Liang Chena, Ching-Hsue Chenga, Hia Jong Teoh, 'Fuzzy time-series based on Fibonacci sequence for stock price forecasting', 2007


1. 예측 방법

• 과거의 주가 데이타를 fuzzy (linguistic) value들의 time-series로 정의합니다.
• 시점 t에서의 fuzzy value를 Lt라고 하면 Lt → Lt+1 처럼 fuzzy value 간의 relation(FLR; Fuzzy Logic Relation)이 식별됩니다. 
• FLR들의 빈도에 따라 가중치를 두어 예측치를 계산합니다.

  간단하게 얘기하면, 오늘의 주가에 대응하는 fuzzy value가 Li 이고, 과거에 발생했던 Li 를 시점으로 하는 FLR들이 Li → Li1, Li → Li2, ..., Li → Lik 일 때, Li1, Li2, ..., Lik 의 defuzzified value들의 가중평균을 내일의 주가 예측치로 사용하는 것입니다.

  위 논문에서는 더 나아가 Fibonacci 수열과 유사한 형태의 식을 활용하여 최종 예측치를 계산하는데요, 그 식은 다음과 같습니다.


2. 예측 equation

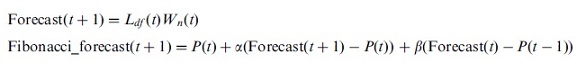그림 1. 예측 Equations

   위의 첫 번째 식이 '1. 예측 방법'에서 설명한 과정을 하나의 식으로 표현한 것입니다. 두 번째 식이 논문의 저자들이 얘기한 Fibonacci 수열입니다.

  이 식에 포함된 상수 α, β는 [-1, 1] 구간의 실수로서 과거 데이터와 그에 대한 예측치 간의 차이, 즉 error measure를 최소화하는 것으로 선택됩니다. (Error measure로는 root mean square error를 사용했습니다.)

  논문에는 상수 α, β를 도출하는 과정에 대한 구체적인 내용이 없이 0.1과 -0.1이 각각 사용되었습니다. 그 값을 그대로 적용하는 것은 이론적으로나 논리적으로 부적절할 것입니다. 그렇다고 다양한 값들에 대해 테스트를 하여 도출하는 것은 무모하리만큼 소모적인 일이겠지요. 그래서 최적화 방법 중의 하나인 Particle Swarm Optimization(PSO) 기법을 구현하여 테스트를 했습니다. 


3. 테스트 결과

  2009년 11월18일부터 2012년 9월6일까지 700개의 LG전자 주가 데이터에 대해 테스트한 결과는 다음과 같습니다.

그림 2. 테스트 결과

  위 그림은 전체 데이터 중 최근 80개 데이터를 차트로 출력한 것입니다. 하늘색 선이 실제 주가의 움직임이고, 붉은색과 녹색이 각각 Fibonacci 수열식을 적용하기 전과 후의 예측 결과입니다.

  관측 기간의 최고가와 최저가는 각각 128,000원, 54,600원이며, 전체 데이터 구간(Universe of discourse)을 54,500에서 128,500까지로 설정하고, 이를 20개의 fuzzy linguistic value로 구분하여 테스트를 수행했습니다. PSO에 의해 도출된 상수 α, β의 값은 각각 -0.1, 0.03이었습니다.


4. 결 론

  그림 1의 두 번째 식, 즉 Fibonacci 수열식을 적용한 예측치 파동의 모양이 실제 주가 파동의 모양과 거의 유사한 것을 그림 2에서 확인할 수 있습니다.

  하지만 파동의 방향이 변하는 지점에서는 실제 파동의 방향과 예측치의 방향이 반대 방향임을 알 수 있습니다. 따라서 실제 주식 매매에 활용하기에는 한계가 있다고 봐야겠습니다.

  이 한계를 극복할 방법을 찾을 수 있을까요? 아니면 일찌감치 다른 예측 모델을 연구해 볼까요?