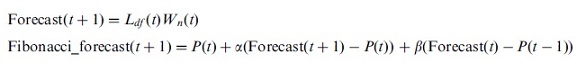Time-Series multiresolution decomposition and forecasting

※ Elliott Pattern Helper Add In

• Download Add In for Excel 2007 ☞
• Download Add In for Excel 2003 ☞

  지난 글에서는  Wavelet multiresolution decomposition을 활용한 financial time-series의 dimensionality reduction에 관하여 언급했었는데요, 예측(forecasting)과 관련하여 wavelet transform에 대한 얘기를 해볼까요?

  Wavelet transform을 예측에 사용하는 방법은 대략 세 가지 정도가 있는데, 첫 번째가  multiresolution analysis를 수행한 후 각각의 resolution에 대한 예측치를 계산하는 것입니다. 두 번째 방법은 wavelet을 기반으로 financial time-series의 noise를 제거한 후 예측을 하는 것이며, 세 번째는 wavelet coefficient들 자체에 예측 알고리즘을 적용하는 것입니다.

  이 중 가장 자주 사용된 방법이 첫 번째 것으로서, financial time-series의 multiresolution decomposition 결과를 활용하는 아주 단순한 방법입니다. 즉, 특정 scale의 approximation layer와 그 보다 작거나 같은 scale의 detail coefficient layer 각각에 대해 예측을 수행하고 inverse transform으로 recostruction함으로써 최종 예측치를 계산하는 것이죠. (Fig 1 참조)

Fig 1. Multiresolution decomposition and forecasting

  이번 글에서는 이와 같은 방법을 담은 과거 발표 논문을 참조하여 실제로 테스트를 수행해 본 결과를 소개하도록 하겠습니다.
 
  ※ 참고 논문: Saif Ahmad, Ademola Popoola, Khurshid Ahmad, 'Wavelet-based Multiresolution Forecasting', 2005.

1. 모델링

   시스템은 크게 세 부분으로 구성됩니다.

• Data preprocessing (Fig 1, 'MODWT')
• Fuzzy rule base (Fig 1, 'Build Fuzzy Rule Base')
• prediction system (Fig 1, 'Provide Forecasts', 'Aggregate Forecasts')

  1.1 Data preprocessing - Multiresolution Decomposition

  Wavelet multiresolution analysis를 수행하여 time-series 데이터의 시간 및 주파수(혹은 주기) 영역 특성을 추출합니다. 쉽게 설명하면, financial time-series를 추세(trend)와 계절적 cycle 및 비즈니스 cycle 등으로 분해하는 것(decomposition)이라고 보시면 됩니다. 

  물론, 현실 세계에서 측정한 time-series에서 추세와 여러 cycle을 정확하게 분리해 내기는 어렵겠지요? 근사치를 얻기 위해 다양한 모형을 개발해 왔으며, wavelet transform을 이용한 multiresolution decomposition은 그 중 하나가 일 뿐입니다.

  논문에서는 Maximal Overlap Discrete Wavelet Transform(MODWT)과 a trous 알고리즘을 적용했습니다. MODWT에 관한 자세한 내용은 위 논문을 참고하시기 바랍니다.

  1.2  Fuzzy rule base - Subtractive Clustering

  Time-series 데이터에 대한 approximation 및 forecasting 시스템으로 Fuzzy Inference System(FIS)을 사용하는데, 이를 위해 fuzzy if-then rule을 생성해야 합니다. FIS의 premise parameter들을 초기화하는 것으로서, 단순하게 생각하면 input 데이터의 범위(universe of discourse)를 patitioning하고 적절한 membership function을 선택하는 과정이라고 볼 수 있습니다.

  대표적인 방법으로 grid partitioning이 있는데요, universe of discourse를 균등하게 분할하고 분할된 구간들에 대해 membership function 종류와 parameter들을 수작업으로 정의하는 것이 일반적입니다.

  Fuzzy if-then rule을 수작업으로 정의해야 하는 경우의 비효율성과 시행착오를 줄이기 위한 효과적인 방법이 data clustering입니다. Input data를 특정 척도(metric)에 따라 다수의 cluster로 구분하고 cluster 당 하나의 rule을 자동으로 정의합니다. Mountain clustering, subtractive clustering 등의 방법이 있으며, 위 논문에서는 subtractive clustering을 사용했습니다.

  1.3 Prediction system - ANFIS

  Multiresolution decomposition의 결과로 생성된 각각의 layer에 대해 예측을 수행하는 FIS로서, training 데이터로 학습(learning)을 시켜 최적화(optimization)시킨 후 실제 데이터에 대해 예측값을 계산하도록 합니다. 

  FIS를 학습(learining)시킨다는 것은 [input, output] 쌍으로 구성된 training 데이터를 FIS에 입력해 가면서 FIS가 계산한 output과 실제 output 간의 차이(error measure)를 줄여나갈 수 있도록 FIS의 내부 parameter들, 즉 premise parameter들과 consequent parameter들을 조정해 나가는 과정을 말합니다.

  학습 알고리즘으로는 gradient descent method처럼 미분을 이용한 방법이 자주 사용되기도 하지만, local maxima를 피하기 위해 particle swarm optimization(PSO), simulated anealing(SA) 등과 같은 derivative-free 방법을 적용하기도 합니다. 2012년 9월의 포스트 'Time-Series Analysis and Forecasting'에서 소개했던 시스템이 PSO를 사용한 것이었습니다.

  논문에서는 First-order (Takagi-Sugeno-Kang) TSK 타입의 FIS를 사용했다고 합니다.

 2. 테스트 시스템

  테스트 시스템은 위 논문에 소개된 아이디어를 적용하여 구성했습니다. 단, prediction system은 2012년 10월에 올렸던 블로그 'ANFIS and Time-Series Forecasting'에서 사용한 ANFIS 시스템을 사용했습니다. ANFIS는 premise parameter들의 최적화에 gradient descent method를, consequent parameter들에 대해서는 least square estimation(최소자승법)을 사용합니다.

  Time-series의 preprocessing 모듈은 엑셀 vba로 Haar a trous 알고리즘을 구현하여 multiresolution analysis를 수행하도록 구성했으며, fuzzy rule base 자동 생성을 위해 subtractive clustering 알고리즘을 C 언어로 구현하여 기존의 ANFIS 모듈과 통합하여 사용할 수 있도록 하였습니다. 엑셀에서 엑셀 vba, vba에서 .exe 파일을 호출하는 구조입니다.

  Time-Series로는 1,000 여개의 KOSPI 지수 데이터를 사용했으며, Fig 1과 같이 scale 5 레벨까지 분해(decomposition)하여  D1, D2,..., D5, S5 등 6개의 layer를 생성하여 테스트를 진행했습니다. 각각의 layer는 maximal overlap DWT를 통해 생성되었으므로 KOSPI 데이터와 동일한 갯수의 데이터를 갖는 time-series입니다. 

  각각의 layer에 대해, FIS는 f(Xk-n, ..., Xk-1) → Xk 처럼 연속된 lagged data만을 input으로 받아 output을 계산하도록 학습됩니다. 그렇게 [input, output] 데이터 쌍을 생성하고, 이들을 90%와 10%로 나누어 각각 training data set과 검증용(check) data set으로 나누어 테스트를 진행했습니다.

3. 테스트 결과

  아래의 Fig 2-1부터 Fig 2-6까지는 scale 5 레벨 decomposition 결과로 생성된 각각의 layer에 대해 예측값을 산출한 결과입니다.

  참고했던 논문에서는 각각의 layer에 대해 FIS의 input dimension을 어떻게 해야 하는지, 즉 몇 개의 lagged data를 input으로 사용해야 하는지에 대한 언급이 없었습니다. 유사한 논문들을 검색하다보니 결국은 '경험적인 방법으로 error measure를 최소화하는 input dimension을 찿는다' 였습니다. 실제로 layer 별로 dimension을 바꿔가며 테스트를 해보니, 'universal approximator'라는 ANFIS 때문인지, 3 이상에서는 별다른 차이가 없음을 알 수 있었습니다. 그래서, 모든 layer에 대해 input dimension을 3으로 설정하여 테스트를 했습니다. 

  Subtractive clustering parameter는 radius 0.2, squash factor 1.25, accept ratio 0.5, reject ratio 0.15를 사용했습니다. 

Fig 2-1. Approximation at scale 5 (S5)

Fig 2-2. Detail coefficients at scale 1 (D1)

Fig 2-3. Detail coefficients at scale 2 (D2)

Fig 2-4. Detail coefficients at scale 3 (D3)

Fig 2-5. Detail coefficients at scale 4 (D4)

Fig 2-6. Detail coefficients at scale 5 (D5)

  위 그림을 보면 D1, D2 처럼 scale이 작은 경우, 즉 주파수가 큰 경우에는 실제값과 예측값 사이의 차이가 눈에 띄게 드러납니다. 하지만, scale이 커질수록 detail layer 또는 approximation layer에 대한 예측 성능이 좋아짐을 알 수가 있군요.

  그렇다면, 모든 layer의 예측값을 합(inverse transfomation)하면 어떻게 될까요?  다음 그림 3이 그 결과입니다.

Fig 3. Reconstruction from forecasts

  지난 몇 개의 포스트에서 소개했던 time-series forecasting 방법들과 마찬가지로  큰 resolution(S5, D5, D4 등)에서는 흐름을 충분히 예측할 수 있습니다. 하지만 D1, D2와 같이 주파수가 높은 layer의 예측 error가 그대로 반영되는 모습입니다. 

  D1을 noise처럼 생각하여 filtering을 한다면 어떻게 될까요? Fig 3보다는 더 정확한 결과를 얻을 수 있는 것이 당연하겠지요.

Fig 4. Reconstruction with D1 filtered

  Fig 3과 4를 비교해 보면 그 차이를 분명히 알 수 있습니다. 논문에서 주장하듯이 Wavelet transform에 의한 time-series preprocessing의 한 가지 이점이 확인되는군요. 

4. 결 론

  정리하면, Wavelet transform 기법으로 time-series를 preprocessing한 후 ANFIS를 사용하여 흐름을 예측해 본 결과, preprocessing의 효용성을 어느 정도 확인할 수 있었습니다. 

  참고논문에서는, 복잡한(complex) time-series를 noise나 계절적 요인 또는 추세를 제거하여 단순화시킴으로써 예측의 정확도를 높일 수 있다고 판단합니다. 실제 D1을 제거한 후의 테스트 결과(Fig 4)는 그 판단의 근거를 뒷받침합니다. 

  한 걸음 더 나아가, 분해된 layer들의 resolution(noise, seasonal, trend 등)에 따라 예측 기법을 상이하게 적용함으로써 예측 효과를 좀 더 향상시킬 수 있지 않을까 기대해 봅니다.

Proof - Gradient of ANFIS w.r.t a premise parameter

※ Elliott Pattern Helper Add In

• Download Add In for Excel 2007 ☞
• Download Add In for Excel 2003 ☞

Neuro-Fuzzy Control and Time-Series Forecasting

※ Elliott Pattern Helper Add In

• Download Add In for Excel 2007 ☞
• Download Add In for Excel 2003 ☞

  이번 글에서는 지난 글에 이어 ANFIS를 사용하여 시계열(time-series) 데이터를 분석하고 그 결과를 기반으로 향후 흐름을 예측하는 방법을 하나 더 소개하겠습니다.

  지금 소개할 방법이 지난 글에 소개된 것과 조금 다른 점은 두 개의 ANFIS를 사용한다는 것입니다. 실제 예측을 수행하는 'Plant'로서의 ANFIS와 이것에 제공될 Control 신호를 생성하는 'Controller' ANFIS가 함께 사용되는 일종의 Neuro-fuzzy contol 형태를 구성하는 방법입니다.

그림 1. Neuro-fuzzy control

  ※ 참고 논문: George S. Atsalakis, Kimon P. Valavanis, 'Forecasting stock market short-term trends using a neuro-fuzzy based methodology', 2009.


1. 모델링

   기본적인 발상은, 주가의 흐름을 아래와 같이 descrete-time 도메인 상의 process-controller equation으로 이해하는 것입니다.

        x(k+1) = f(x(k), u(k))
        u(k) = g(x(k))

  시간 k+1에서의 주가 x(k+1)은 시간 k에서의 주가 x(k)와 control signal u(k)에 의해 결정되며, 궁극적인 문제는 x(k)로부터 u(k)를 찾는 것입니다.

  위 논문에서 사용된 controller ANFIS의 training data set은 [x(k), x(k+1); u(k)]입니다. x(k)와 x(k+1)은 각각 시간 k와 k+1에서의 주가의 변화이며, u(k)는 |x(k) - x(k+1)|입니다. Membership function은 Gaussian 2로 각각의 input에 대해 5 개, 총 25 개의 inference rule로 400 epoch 동안 training을 수행했습니다.

  예측을 수행하는 plant ANFIS에서 사용할 signal u(k)의 값은 learning 이후의 controller ANFIS에서 input (x(k), xd(k+1))에 대해 계산한 output입니다. 여기서, xd(k+1)은 시간 k+1에서의 주가의 변화 x(k+1)을 미리 알 수 없기 때문에 사용한 값으로서, 시행착오 끝에 시간 k에서의 3일 이동평균 변화량을 채택했다고 합니다.

  주식시장의 프로세스 모델이라고 볼 수 있는 plant ANFIS는 data set [x(k-1), x(k), u(k); x(k+1)]으로 training한 후, 예측을 수행하도록 했습니다. 각각의 input에 대해 Gaussian 2 membership function을 3 개씩, 총 27 개 rule로 100 epoch 동안 training했습니다.


2. 테스트 시스템

  위 논문에 소개된 neuro-fuzzy control 모델을 그대로 적용하였으며, membership funciton만 Gaussian 2가 아닌 Gauss membership function을 사용하여 테스트했습니다.

  테스트 데이터로는 680 여개의 KODEX 레버리지 지수 데이터를 사용했으며, 이를 90%와 10%로 나누어 각각 training data set과 검증용(check) data set으로 나누어 테스트를 진행했습니다. 


3. 테스트 결과

  아래 그림 2는 controller ANFIS에 의한 output입니다. Training data set에 대해서는 실제 u(k)와 계산된 u(k) 값이 거의 일치하는 것처럼 보입니다. 물론 마지막 input (x(k), xd(k+1))의 output은 실제 값과는 차이가 나는 것을 볼 수 있으며, 이는 당연한 결과일 것입니다. 

그림 2. Controller ANFIS Output

  다음 그림은 plant ANFIS를 100 epoch 동안 training하는 과정에서의 learning error 변화를 나타낸 것입니다.

그림 3. Plant ANFIS의 epoch 별 에러 추이

  위 결과에 따라 epoch 수를 72회로 조정하여 plant ANFIS를 다시 training했습니다. 다음은 controller ANFIS가 산출한 u(k)를 input signal로 받아 plant ANFIS가 예측한 output, 즉 x(k+1) = f(x(k-1), x(k), u(k))를 실제 주가 흐름과 대비하여 표시한 그림입니다. 

그림 4. Plant ANFIS Output

  위 그림 3의 결과를 보면 '모양은 비슷해 보이지만.., 한 발 늦는군...'요. 논문에서는 4,000여 개가 넘는 data로 training한 후 60%가 넘는 'hit ratio' 결과를 얻었다고 하는데요, 위 결과는 그에 미치지 못했습니다. Training data의 양을 늘려야 할까요..?

4. 결 론

  정리를 하면, 주식 시장의 프로세스 모델을 아래 식에 기반한 neuro-fuzzy control로 모델링하여 주가의 단기 흐름을 예측해 보았습니다.

        x(k+1) = f(x(k-1), x(k), u(k))
        u(k) = g(x(k))

  Control signal u(k)는 3일 이동평균 변화량에 대한 controller ANFIS의 output입니다. 

  위 참고논문에서는 연구 성과를 타 연구들과 대비하여 'Hit Ratio가 조금 더 낫다'라고 스스로 평가하고 있습니다. Hit ratio 60% 정도면 'Random Walk'보다는 좋겠지요...? 

  물론, 제가 직접 테스트한 결과 수치는 그 정도까지 나오진 않았습니다만 training data의 양을 크게 증가시키고 동일한 membership function을 사용한다면 더 좋은 결과가 나올 수도 있을 것입니다.

ANFIS and Time-Series Forecasting

※ Elliott Pattern Helper Add In

• Download Add In for Excel 2007 ☞
• Download Add In for Excel 2003 ☞

  지난 9월의 한 글에서 시계열(time-series) 데이터를 분석하고 그 결과를 기반으로 향후 흐름을 예측하는 방법을 하나 소개했었지요. 그 방법은 과거의 주가 흐름을 단순한 형태의 Fuzzy time series로 구조화(Fuzzy Inference System, 이하 FIS)하여 분석하는 것이었습니다.

  이번 글에서는 신경망(Neural Network, 이하 NN) 기반의 인공지능(Artificial Intelligence, 이하 AI) 기법을 이용한 주가 예측 방법을 한 가지 소개하고, 실제 구현하여 테스트한 결과를 공개합니다. 

  이 또한 과거에 발표되었던 논문을 기준으로 한 것이며, 이 방법에 의한 예측 결과를 실제 투자의 기준으로 활용하는 것은 부적절할 수 있음을 미리 알립니다.

  ※ 참고 논문: George S. Atsalakis, Emmanouil M. Dimitrakakis, Constantinos D.Zopounidis, 'Elliott Wave Theory and neuro-fuzzy systems, in stock market prediction: The WASP system', 2011.


1. 기술적 배경

  분석에 사용한 이론적·기술적 방법은 ANFIS, 즉 Adaptive Network-based Fuzzy Inference System(이하 ANFIS)입니다.

  일종의 FIS인데요, 그 내부에서 사용되는 membership function(이하 MF)의 parameter들을 NN의 자기학습(learning)으로 최적화함으로써 예측이나 분류 등 다양한 분석 분야에 사용됩니다.

• Fuzzy inference system

  보통 우리가 알고 있는 함수들은 input이 가령 x = 3, y = 4일 때 output z = x^2 + y^2 = 5^2이다...처럼 실수나 복소수 값(crisp value)들을 사용합니다. 그런데 이를 전제로 하는 함수 또는 식으로 모든 시스템을 simulation할 수는 없습니다.

  특정 분야의 어떤 전문가들은 가령 수온이 꽤 높을 때 밸브를 잠근다...처럼 오랜 경험에 기초하여 시스템을 운영하기도 합니다. 이러한 전문가들의 행위를 자동화한다면 시스템을 어떻게 모델링해야 할까요? 수온이 꽤 높다...? 80도? 90도? 어떤 특정 값으로 정의하기는 어렵습니다.

  이런 문제들을 모델링하기 위해 나온 것이 fuzzy value(또는 fuzzy set)라는 개념과 이에 기초한 FIS입니다.

  FIS는 input과 output으로 crisp value가 아닌 fuzzy value를 갖는 다수의 룰(inference rule, 함수에 대응)을 정의함으로써 시스템을 모델링 합니다. 그런데, fuzzy value는 MF로 정의됩니다. 가령 '꽤 높다'라는 fuzzy value는 수온에 대해 10℃를 0으로, 20℃ → 0, ..., 60℃ → 0, 70℃ → 0.5, 80℃ → 1, 90℃ → 1, 100℃ → 1 등으로 대응시키는 함수, 즉 MF(그림 1 참조)로 정의할 수 있습니다.

그림 1. Membership function

  따라서 어떤 시스템을 FIS로 모델링 또는 simulation 한다는 것은 input과 output을 몇몇 MF로 정의하고 이들 사이의 대응관계, 즉 inference rule을 찾는 것입니다. 

• Neural network

  인공지능(AI)이나 신경망(NN)에 대한 구체적인 거론은 기회가 되면 하기로 하구요, ANFIS와 관련해서 필요한 사항만 언급하겠습니다.

  특정 시스템을 FIS로 구현하려면, 위에서 얘기했듯이 다수의 MF를 정의해야 합니다. 그런데, 시스템의 input과 output을 정의하는 것 뿐만 아니라 MF와 inference rule을 찾는 데에도 해당 분야의 전문적인 지식이 필요하며, 수많은 시행착오를 겪을 수밖에 없습니다.

  MF는 주어진 input에 대해 0에서 1 사이의 값인 membership grade를 대응시킵니다. 대표적인 형태로 triangle, trapezoid, gaussian, bell 및 sigmoid 등이 있는데, 각각의 형태에 대해 구체적인 모양을 규정하는 parameter들이 존재합니다. 이들을 premise parameters라고 합니다. 각각의 inference rule 또한 최종 output을 산출하기 위해 몇몇 parameter들을 사용하는데요, 이들은 consequent parameters라고 불립니다. (그림 2의 pi, qi, ri 등)

그림 2. ANFIS

  FIS를 정의하는 이 parameter들을 찾기 위해, ANFIS는 노력과 시행착오를 줄이기 위한 방편으로 NN의 자기학습(learning) 기법을 사용합니다.

  2. 시스템 모델링

   모델링 대상은 time-series로서 KOSPI 종목 LG전자 주가의 흐름이며, 시스템의 input과 output은 위 논문의 내용을 따릅니다. 아이디어를 간략히 기술하면, 3일 동안의 Elliott wave oscillator(이하 EWO) 흐름으로 주가 흐름을 예측하는 것으로서, EWO가 (+)에서 (-)로 또는 (-)에서 (+)로 바뀔 때를 의미있는 진입시점으로 관측하기 위함입니다.

• Input: 3일간의 Elliott wave oscillator (EWOt-2, EWOt-1, EWOt)
• Output:(t+1)일의 주가 흐름 (if positive rate of change then 1, else -1)

  각각의 input에 대한 membership function의 갯수는 2개로서 '높다'와 '낮다' 두 개의 fuzzy value만을 사용하는 것입니다.

  논문에서는 MF를 이런 저런 형태로 바꿔가면서, NN의 step size(learning과 관련된 parameter)를 다양한 값으로 변경해가며, 총 42개의 ANFIS 모델을 사용했다고 합니다. 테스트 데이터(training data set)에 대해 학습을 수행한 후 에러율이 낮은 모델을 선택하여 예측치를 산출하고 그 결과를 바탕으로 진입/청산을 한 것이지요. 자세한 내용은 논문을 참조하시기 바랍니다.

  이 글은 위 논문의 아이디어를 LG전자 종목에 대해 제가 구현한 테스트 시스템을 사용하여 몇몇 MF type으로 테스트한 결과를 포함합니다.


3. 테스트 시스템 구축

  테스트 시스템은 Ubuntu(VirtualBox guest)에서 GNU Scientific Library(GSL)를 사용하여 개발한 후, Windows용으로 porting하여 향후 Elliott Pattern Helper에서 활용할 수 있도록 했습니다.

  이 과정에서 GSL을 Windows용으로 porting해야 했는데요, 다행히도 Visual Studio용 솔루션 파일을 구할 수 있었습니다. 이것을 이용하여 Visual Studio 2012 Express에서 GSL을 porting 했습니다.

• GNU Scientific Library on Visual Studio 2012 Express

  테스트 데이터로는 2008년 6월 10일부터 2012년 10월 5일까지 총 1,084개의 LG전자 주가 데이터를 사용했으며, 이를 NN의 training data set과 검증용(check) data set으로 나누어 테스트를 수행했습니다. 


4. 테스트 결과

  Training data set으로는 전체 1,084 개의 데이터 중 50%를 사용하고 나머지 50%를 검증에 사용했습니다. 

  반복 learning 횟수(epochs)는 MF 별로 over fitting으로 인한 error measure의 상승이 관측되기 전까지로 했으며, error measure로는 Root Mean Square Error(이하 RMSE)를 사용했습니다. 

  결과는 실제 주가의 흐름(상승 또는 하락)과 ANFIS의 계산 결과(+ 또는 -)를 단순비교하여 백분율로 표시하겠습니다.

• Gauss MF, 500 Epochs

그림 3. Epoch별 RMSE 추이 - Gauss MF

             ▶ 결과: training data set: 57%
                          check data set:   49%

• Bell MF, 240 Epochs

그림 4. Epoch별 RMSE 추이 - Bell MF

             ▶ 결과: training data set: 52%
                          check data set:   52%

• Triangle MF, 300 Epochs

그림 5. Epoch별 RMSE 추이 - Triangle MF

             ▶ 결과: training data set: 52%
                          check data set:   50%

• Trapezoid MF, 64 Epochs

그림 6. Epoch별 RMSE 추이 - Trapezoid MF

             ▶ 결과: training data set: 57%
                          check data set:   46%

• Sigmoid MF, 200 Epochs

그림 7. Epoch별 RMSE 추이 - Sigmoid MF

             ▶ 결과: training data set: 45%
                          check data set:   45%

5. 결 론

  Training data set에 대해서는 최고 57%의 결과를 얻었지만, learning 이후 실제 예측에서는 최고 52%로 그리 만족할만한 수치가 아니군요. Training data set의 비율을 70%, 80%로 늘려도 결과는 거의 비슷하게 나왔습니다.

  소득이 있다면, MF의 종류에 따라 그 결과가 확연히 다르다는 것을 알 수 있었다는 것입니다. 그렇다면 MF의 수를 달리하면 어떻게 될까요..? 그리고, LG전자가 아닌 다른 종목에 대해 테스트를 하면 어떻게 될까요..?

  우선은 ANFIS 테스트 시스템을 구축한 것으로 만족해야 겠습니다. 이후에는 input과 output을 EWO나 주가 등락이 아닌 다른 변수로 바꾸어가며 테스트를 해보고 그 결과를 올리도록 하겠습니다.

Elliott Pattern Helper (EPH) 1.0 QuickStart - Installation and Setting

1. EPH Excel Add-In 다운로드

• Download Add In for Excel 2007 ☞
• Download Add In for Excel 2003 ☞

2. EPH Add-In을 Excel AddIns 디렉토리에 저장

  AddIns 디렉토리의 위치는, 엑셀 실행 → Alt + F11 (Visual Basic 편집창) → Ctrl + G ('직접 실행(Immediate Window)' 창) → 'MsgBox Application.UserLibraryPath' 입력 후 엔터키를 누르면 확인할 수 있습니다.


3. EPH Add-In 설치

• Excel 2007의 경우

3-1. Excel을 실행시킨 후 Excel 옵션창을 띠웁니다.

그림 1. Add In 설치 1

3-2. '추가 기능'을 클릭합니다.

그림 2. Add In 설치 2

3-3. 아래 그림과 같이 '이동' 버튼을 클릭합니다.

그림 3. Add In 설치 3

3-4. 'Elliott Pattern Helper' 체크박스를 설정한 후 '확인' 버튼을 클릭합니다.

그림 4. Add In 설치 4

3-5. 엑셀 시트 위에서 마우스 오른쪽 버튼을 클릭하여 컨텍스트 메뉴를 띄우면 추가된 Elliott Pattern Helper의 메뉴들이 생성된 것을 확인할 수 있습니다.

그림 5. Add In 설치 완료

•  Excel 2003의 경우

3-1. Excel을 실행한 후 아래 그림과 같이 '도구'(Tools) 메뉴의 '추가 기능'(Add-Ins)을 선택합니다.

그림 6. Add-In 설치 1

3-2. Add-Ins 설정창에서 사용가능한 Add-In 목록(Add-Ins available)에 'Elliott Pattern Helper'가 있는지 확인합니다.

그림 7. Add-In 설치 2

3-3. 아래 그림과 같이 'Elliottpatternhelper2003' 체크박스를 선택한 후 '확인'(OK) 버튼을 클릭합니다.

그림 8. Add-In 설치 3

3-4. Excel 시트 위에서 마우스 오른쪽 버튼(왼손 마우스의 경우 왼쪽 버튼)을 클릭했을 때  팝업되어 나오는 컨텍스트 메뉴에 아래 그림과 같이 EPH 메뉴가 보일 경우 EPH Add-In이 제대로 설치된 것입니다.

그림 9. Add In 설치 완료

4. EPH 설정

  아래 그림 10과 같이  Data Helper → Settings를 선택하여 'Elliott Pattern Helper Settings' Form을 실행시킵니다.

그림 10. EPH 설정 1

4.1 Labels 설정

  'Labels' Pane의 Date, Volume, Open, High, Low 및 Close 필드에 대응되는 주가 데이터 항목을 각각 입력합니다.

그림 11. Labels 설정 1

 
  대응되는 주가 데이터 항목이란 아래 그림과 같이 증권사 HTS를 통해서 저장한 주가(또는 지수) 데이터의 헤더에 포함된 데이터 항목의 이름을 말합니다.

그림 12. Labels 설정 2

  'Labels' Pane의 'Tick V', 'Tick T' 필드는 DDE 연동을 위한 Sheet('_Quote' sheet) 생성 시 참조하는 DDE Item 항목에 대한 이름으로서 어떤 값을 입력해도 무방합니다.
 
  'Save' 버튼을 클릭하여 설정 내용을 저장합니다.

4.2 Elliott Oscillator 설정

  Elliott Wave Oscillator는 5/35 또는 5/34 MACD oscillator를 말합니다. 아래와 같이 'Elliott Oscillator' Pane에서 oscillator와 signal에 사용될 주기(Period)에 대한 설정을 합니다.

그림 13. Elliott Oscillator 설정

  'MA to use' 콤보 박스는 이동평균 계산에 사용될 기준 가격(또는 지수)을 설정하기 위한 것으로서, 종가를 사용하려면 'Close Values'를 선택하면 됩니다. 고가와 저가의 평균가를 기준가로 사용하려면 'Average Values'를 선택합니다.

  EPH는 두 종류의 차트 기능을 제공합니다. 그 중 하나는 Fractal Counting 차트로서 Oscillator를 포함합니다. 다른 하나는 Wave Structure 차트인데, 이 차트를 출력할 때 Elliott Oscillator를 포함시키려면 'Elliott Chart displays an oscillator' 체크박스를 선택합니다.

4.3 Counting 설정

  EPH는 Elliott wave fractal counting과 oscillator 및 단순 wave counting 결과를 출력하는 Fractal Counting 차트 기능을 제공합니다. 이를 위한 설정을 'Counting' Pane에서 아래와 같이 수행합니다.

그림 14. Counting 설정

  'Chart Type'은 캔들 차트의 종류를 말하는 것으로서 OHLC(Open-High-Low-Close)나 HLC(High-Low-Close) 중 기호에 따라 선택합니다.

  'Consecutive fractals' 콤보박스는 같은 종류(up 또는 down)의 fractal이 연속해서 나타날 때 어떻게 처리할 것인가에 대한 설정을 하기 위한 것입니다. 모두 count하거나 skip할 수 있습니다. Skip은, 연속된 up fractal의 경우 고가가 더 높은 fractal만 count하고, 연속된 down fractal의 경우 저가가 더 낮은 fractal만 count하는 것을 말합니다.

  'Oscillator Type'은 Fractal Counting 차트에 포함될 oscillator의 종류를 선택하기 위한 것입니다. Elliott oscillator나 Williams' MFI 중 하나를 선택합니다. ※ Williams' MFI에 대한 내용은 Bill Williams의 저서를 참고하십시요.

  'Wave Counting'은 up fractal 또는 down fractal의 추세(상승 또는 하락) 변화를 자동으로 count할 것인지를 설정하기 위한 것입니다.

  'Number of Candles'는 fractal formation의 time window를 정의하기 위한 것입니다. 가령, 일봉이나 주봉 또는 그 이상의 차트의 경우 일반적으로 5-bar formation을 사용하며, 분 단위 차트의 경우 7-bar, 9-bar 또는 더 큰 formation을 적절히 사용합니다.

4.4 Chart Size 설정

  'Chart Size' Pane에서 EPH를 통해 생성되는 모든 차트들에 대해 크기와 위치 속성을 설정합니다.

그림 15. Chart Size 설정

  'Chart Size (W×H)' 필드에 차트의 폭(Width)과 높이(Height)를 설정합니다.

  'Monowave Chart' 필드에는 Pattern Helper → Wave Structure 메뉴를 통해 출력되는 부분 차트의 폭과 높이를 각각 설정합니다. 이 차트의 경우 위치 속성은 정의할 수 없습니다.

  'Chart Position (XY)' 필드에는 차트의 X-position과 Y-position을 각각 설정합니다. 마지막으로 'Number of Candles' 필드에는 차트에 포함될 캔들(또는 bar)의 수를 설정합니다.

  'Save' 버튼을 클릭하여 설정 내용을 저장합니다.

5. 주식 종목코드(Stock Code) 적재

  증권사 HTS의 DDE 기능을 연동하여 종목이나 지수의 실시간 체결정보(체결량, 체결시간)를 엑셀로 축적하기 위해 종목코드를 EPH에 저장합니다.

  ※ DDE 연동 기능을 사용하지 않을 경우 이 작업을 생략할 수 있습니다.
  ※ 이 작업은 EPH 설치 후 한 번만 수행하면 됩니다. 물론, 신규 상장/등록되는 종목들의 목록을 등록해야 할 경우 다시 수행해야 합니다.

그림 16. 종목코드 적재 1

  위 그림과 같이 HTS를 통해 종목코드 목록을 엑셀 시트로 복사한 후, EPH의 Data Helper → Save Stock Codes 메뉴를 실행합니다.

그림 17. 종목코드 적재 2

  위 화면과 같이 'Loading Stock Codes' form에 종목코드 열과 종목명 열을 각각 지정하여 'Save' 버튼을 클릭하면 종목코드 목록이 EPH에 저장됩니다.

Time-Series Analysis and Forecasting

  시계열(time-series) 데이터를 분석하고 그 결과를 기반으로 향후 흐름을 예측하고자 하는 노력은 다양한 분야에서 지속적으로 이루어져 왔습니다. 주가 예측도 마찬가지겠지요.

  이번 글에서는 주가 예측을 위한 한 가지 방법을 소개하고, 실제 구현하여 테스트한 결과를 공개하고자 합니다. 과거에 발표되었던 논문을 기준으로 한 것이며, 이 방법에 의한 예측 결과를 실제 투자의 기준으로 활용하는 것은 부적절함을 미리 알립니다.

  ※ 참고 논문: Tai-Liang Chena, Ching-Hsue Chenga, Hia Jong Teoh, 'Fuzzy time-series based on Fibonacci sequence for stock price forecasting', 2007


1. 예측 방법

• 과거의 주가 데이타를 fuzzy (linguistic) value들의 time-series로 정의합니다.
• 시점 t에서의 fuzzy value를 Lt라고 하면 Lt → Lt+1 처럼 fuzzy value 간의 relation(FLR; Fuzzy Logic Relation)이 식별됩니다. 
• FLR들의 빈도에 따라 가중치를 두어 예측치를 계산합니다.

  간단하게 얘기하면, 오늘의 주가에 대응하는 fuzzy value가 Li 이고, 과거에 발생했던 Li 를 시점으로 하는 FLR들이 Li → Li1, Li → Li2, ..., Li → Lik 일 때, Li1, Li2, ..., Lik 의 defuzzified value들의 가중평균을 내일의 주가 예측치로 사용하는 것입니다.

  위 논문에서는 더 나아가 Fibonacci 수열과 유사한 형태의 식을 활용하여 최종 예측치를 계산하는데요, 그 식은 다음과 같습니다.


2. 예측 equation

그림 1. 예측 Equations

   위의 첫 번째 식이 '1. 예측 방법'에서 설명한 과정을 하나의 식으로 표현한 것입니다. 두 번째 식이 논문의 저자들이 얘기한 Fibonacci 수열입니다.

  이 식에 포함된 상수 α, β는 [-1, 1] 구간의 실수로서 과거 데이터와 그에 대한 예측치 간의 차이, 즉 error measure를 최소화하는 것으로 선택됩니다. (Error measure로는 root mean square error를 사용했습니다.)

  논문에는 상수 α, β를 도출하는 과정에 대한 구체적인 내용이 없이 0.1과 -0.1이 각각 사용되었습니다. 그 값을 그대로 적용하는 것은 이론적으로나 논리적으로 부적절할 것입니다. 그렇다고 다양한 값들에 대해 테스트를 하여 도출하는 것은 무모하리만큼 소모적인 일이겠지요. 그래서 최적화 방법 중의 하나인 Particle Swarm Optimization(PSO) 기법을 구현하여 테스트를 했습니다. 


3. 테스트 결과

  2009년 11월18일부터 2012년 9월6일까지 700개의 LG전자 주가 데이터에 대해 테스트한 결과는 다음과 같습니다.

그림 2. 테스트 결과

  위 그림은 전체 데이터 중 최근 80개 데이터를 차트로 출력한 것입니다. 하늘색 선이 실제 주가의 움직임이고, 붉은색과 녹색이 각각 Fibonacci 수열식을 적용하기 전과 후의 예측 결과입니다.

  관측 기간의 최고가와 최저가는 각각 128,000원, 54,600원이며, 전체 데이터 구간(Universe of discourse)을 54,500에서 128,500까지로 설정하고, 이를 20개의 fuzzy linguistic value로 구분하여 테스트를 수행했습니다. PSO에 의해 도출된 상수 α, β의 값은 각각 -0.1, 0.03이었습니다.


4. 결 론

  그림 1의 두 번째 식, 즉 Fibonacci 수열식을 적용한 예측치 파동의 모양이 실제 주가 파동의 모양과 거의 유사한 것을 그림 2에서 확인할 수 있습니다.

  하지만 파동의 방향이 변하는 지점에서는 실제 파동의 방향과 예측치의 방향이 반대 방향임을 알 수 있습니다. 따라서 실제 주식 매매에 활용하기에는 한계가 있다고 봐야겠습니다.

  이 한계를 극복할 방법을 찾을 수 있을까요? 아니면 일찌감치 다른 예측 모델을 연구해 볼까요?